Che cos’è e in cosa consiste uno studio GAGE R&R?
GUIDA INTRODUTTIVA

In questa Guida introduttiva (parte 2 di 2) vogliamo introdurre il concetto di studio Gage R&R, inteso come strumento per la valutazione dell’adeguatezza di un sistema di misura.
Deviazioni del sistema di misura infatti possono influenzare l’accuratezza e la precisione della misura stessa.
Il Gage R&R consente di fare una stima delle deviazioni di RIPETIBILITA’ e della RIPRODUCIBILITA‘ sulla varianza generale della misura.
Richiedici informazioni su come è possibile gestire gli strumenti di misura (anagrafica, spostamenti, calibrazioni) e il Gage R&R con il sistema QMS 1FACTORY
5. Panoramica dello studio Gage R&R ad attributo
Uno studio Gage R&R ad attributo coinvolge più operatori, pezzi e misure ripetute della stessa parte da ciascun operatore (chiamiamo queste misure ripetute “prove”). È solito avere 3 operatori, 30 pezzi e 3 prove su ogni pezzo. Gli operatori registrano una semplice misurazione Pass/Fail (cioè Attributo).
(In casi più complessi, gli operatori potrebbero dover classificare i pezzi in categorie, ad esempio Classe A, Classe B e Classe C).
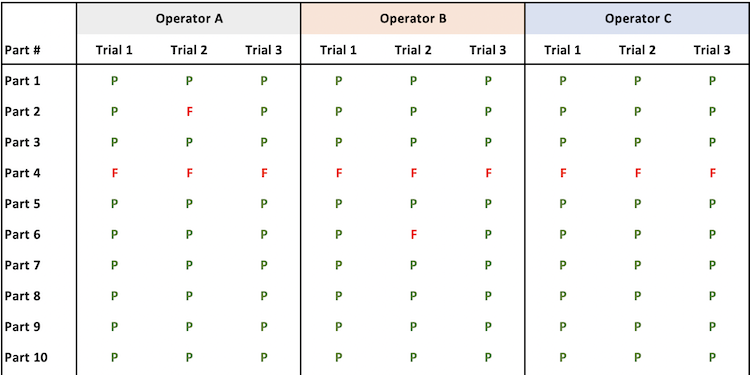
IMPORTANTE: in uno studio Gage R&R ad attributi, il disaccordo all’interno delle prove di ciascun operatore e i disaccordi tra gli operatori saranno evidenti solo nei pezzi che sono vicini al limite superiore di specifica (USL) e al limite inferiore di specifica (LSL).
6. Calcoli Gage R&R ad attributo
La valutazione di ciascun operatore (Pass/Fail) viene confrontata con la valutazione (Pass/Fail) degli altri due operatori e con un valore di riferimento. Il valore di riferimento deve essere ottenuto da un sistema di misurazione variabile affidabile (ad esempio, una CMM, un dispositivo di misurazione del colore, ecc.) o da un perito esperto.
Ripetibilità: Per ogni operatore misuriamo quante volte arriva alla stessa valutazione in ogni prova (cioè, le misure di ogni operatore per lo stesso pezzo sono coerenti?). Dividiamo poi questo numero per il numero totale di pezzi per ottenere la percentuale di ripetibilità. Se le misure dell’operatore sullo stesso pezzo sono coerenti per meno del 90% del tempo, l’operatore deve essere ri-formato.
Riproducibilità: Misuriamo quindi quante volte gli operatori concordano con le rispettive misure individuali (cioè, le misure dello stesso pezzo sono coerenti tra gli operatori?). Dividiamo poi questo numero per il numero totale di pezzi per ottenere la percentuale di riproducibilità.
7. Panoramica sullo studio Gage R&R a strumento variabile
Lo studio Gage R&R a strumento variabile (incrociato) coinvolge più operatori, pezzi e misure ripetute della stessa parte da ciascun operatore (chiamiamo queste misure ripetute “prove”).
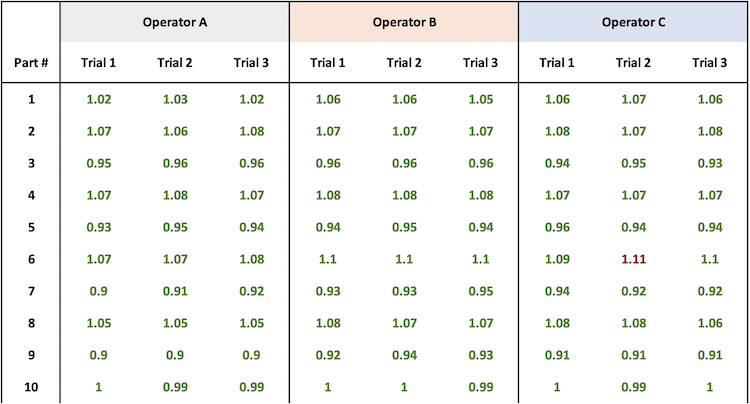
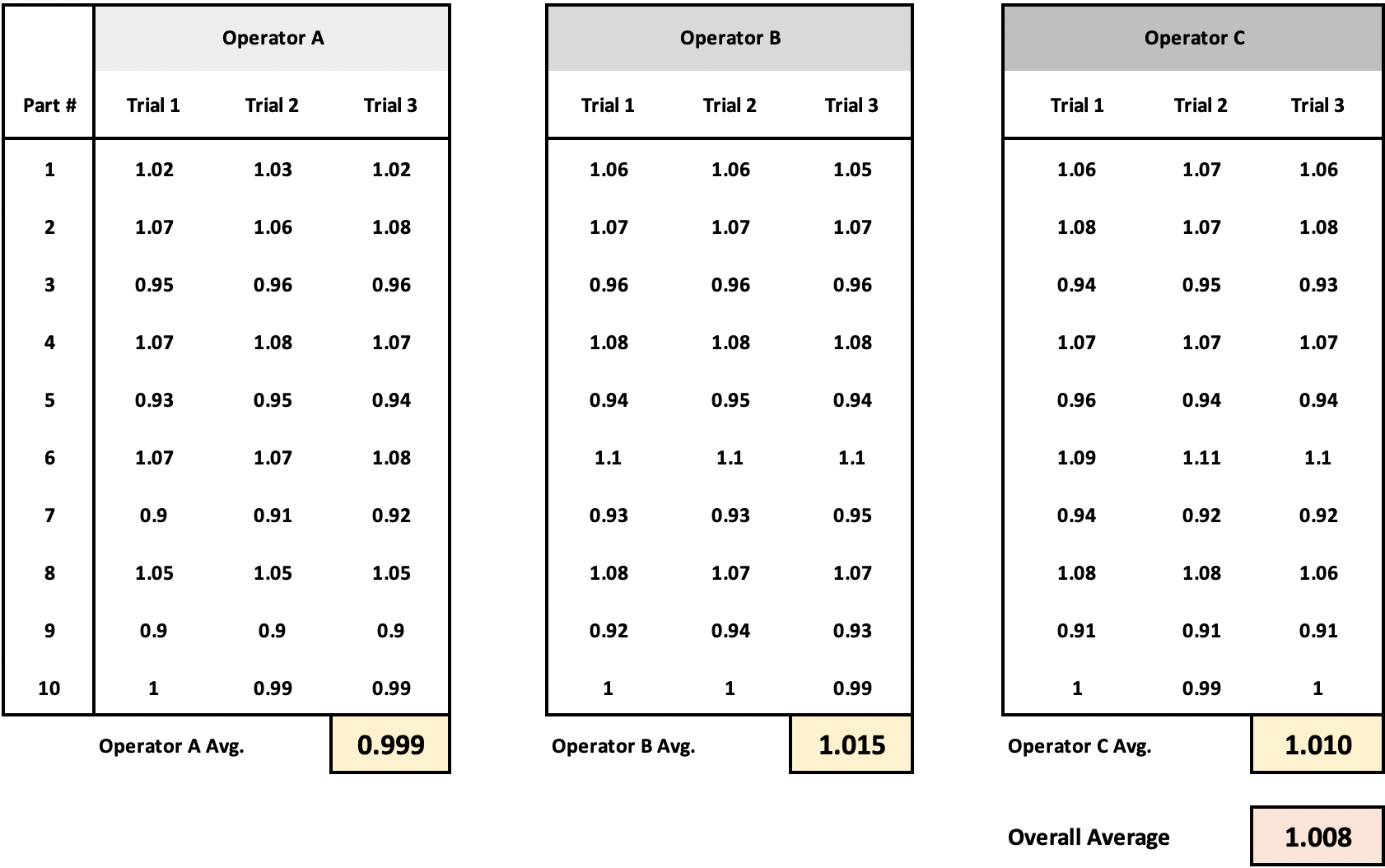
È comune avere 3 operatori (k), 10 pezzi (n) e 3 prove (r) su ogni pezzo. Ogni operatore misura ogni pezzo tre volte, registra il valore numerico (cioè variabile) della misura e si ottiene una tabella come quella mostrata qui.
8. ANOVA, Analisi della varianza
Il primo passo consiste nel calcolare la variazione totale. Ma una volta ottenuta la variazione totale, come facciamo a sapere quale frazione della variazione deriva dai pezzi stessi e quale dall’operatore o dallo strumento?
È qui che si rivela utile la tecnica ANOVA (Analisi della varianza). Essa ci permette di suddividere la variazione in fattori.
Variabilità totale = Variabilità delle parti + Variabilità degli operatori + Variabilità delle attrezzature + Variabilità dell’interazione tra operatore e strumento
SSTotale = SSParti + SSOperatore + SSEquipaggiamento +SSInterazione
9. Variazione totale
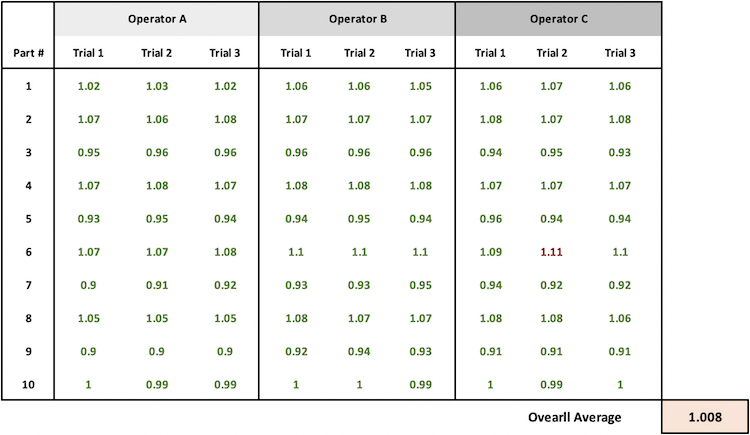
Per calcolare la variazione totale, si calcola la somma dei quadrati della differenza tra ciascun valore misurato e la media complessiva. Si tratta della somma totale dei quadrati (SS-Total).
Ad esempio:
L’errore quadratico per “Operatore A – Parte 1 – Prova 1” è (1,02 – 1,008)2 = (0,012)2 = .000144
L’errore quadratico per “Operatore B – Parte 8 – Prova 2” è (1,07 – 1,008)2 = (0,062)2= .003844
10. ANOVA e componenti della variazione
L’ANOVA utilizza un trucco molto semplice per calcolare la frazione di variabilità delle parti, degli operatori e delle attrezzature. Raggruppiamo il set di dati in modi diversi per esaminare se le differenze di misura sono tra parti (desiderate), o tra operatori (un problema di riproducibilità), o tra prove (un problema di ripetibilità).
I raggruppamenti di interesse sono quattro:
Raggruppamento per parti
Raggruppamento per operatori (riproducibilità)
Raggruppamento per operatore e per parte, cioè per apparecchiatura (ripetibilità).
11. Raggruppamento per parti
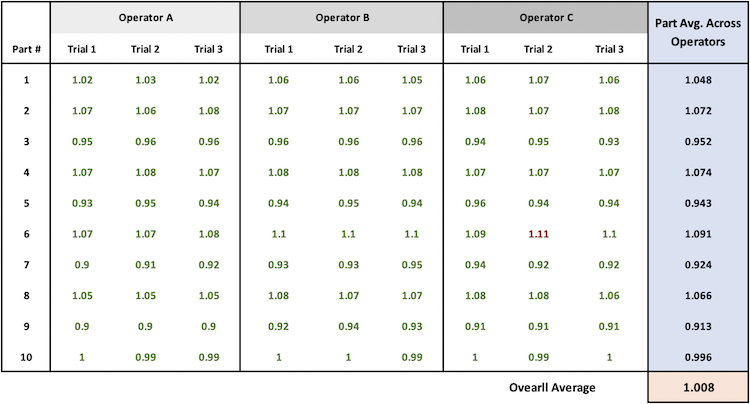
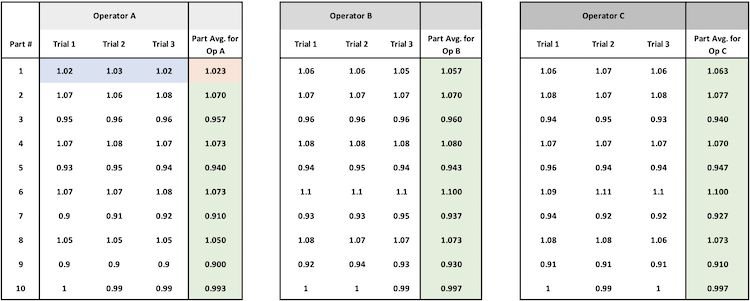
Idealmente, tutta la variazione deriva dalle parti stesse. Ci aspettiamo quindi di vedere un’elevata quantità di variazione tra i pezzi. Per determinare quanta variazione deriva dai pezzi, raggruppiamo i dati per parte e calcoliamo la media per ogni parte. Quindi confrontiamo la media di ciascuna parte con la media complessiva.
Si tratta della somma del quadrato della differenza tra la media di ogni parte e la media generale. Ci sono 10 parti e calcoliamo 10 termini di errore quadratico che sommiamo per ottenere le SS-Parte.
Ad esempio:
L’errore quadratico per la Parte 1 è (1,048 – 1,008)2 = (0,04)2 = .0016
L’errore quadratico per la Parte 7 è (.924 – 1.008)2 = (-0.084)2= .0070
Si noti il segno negativo nel calcolo dell’errore per la Parte 7. Eleviamo al quadrato i valori dell’errore per eliminare il segno negativo. Poi sommiamo tutti i valori al quadrato.
12. Raggruppamento per operatore (riproducibilità)
Per determinare quanta variazione deriva dagli operatori, raggruppiamo i dati per operatore e calcoliamo la media per ogni operatore. Quindi confrontiamo le medie di ciascun Operatore con la media complessiva.
Si tratta della somma dei quadrati della differenza tra la media di ciascun operatore e la media generale. Ci sono 3 operatori e si calcolano 3 termini di errore quadratico che vengono sommati per ottenere SS-Operatori.
L’errore quadratico per l’operatore A è (0,999 – 1,008)2 = (-0,009)2 = .000081
L’errore quadratico dell’operatore B è (1,015 – 1,008)2 = (.007)2= .000049
L’errore quadratico dell’operatore C è (1,010 – 1,008)2 = (,002)2= .000004
13. Raggruppamento per operatore e pezzo (ripetibilità)
La quantificazione della misura dell’apparecchiatura richiede un altro confronto. Questa volta per determinare quanta variazione deriva dall’apparecchiatura, raggruppiamo i dati per operatore e pezzo. Questo raggruppamento ci fornisce solo la variazione dell’apparecchiatura, perché è lo stesso operatore a misurare lo stesso pezzo per tre volte.
Il risultato è la somma del quadrato della differenza tra ogni misura operatore-parte e la media operatore-parte corrispondente. Esistono 30 combinazioni operatore-parte e si calcolano 30 termini di errore quadratico che vengono sommati per ottenere SS-attrezzatura.
Ad esempio:
L’errore quadratico per “Operatore A – Parte 1 – Prova 1” è (1,02 – 1,023)2 = (-0,003)2= .000009
L’errore quadratico per “Operatore A – Parte 1 – Prova 2” è (1,03 – 1,023)2 = (-0,007)2= .000049
L’errore quadratico per “Operatore A – Parte 1 – Prova 3” è (1,02 – 1,023)2 = (-0,003)2= .000009
14. Interazione tra operatore e strumento
La somma dei quadrati dell’interazione viene calcolata sottraendo da SSTotale i valori di SSParts, SSOperator e SSEquipment.
SSInterazione = SSTotale – SSParts – SSOperator – SSEquipment





